Appendix: CE-1p

The CE-1p (CrystalExplorer 1-parameter) model provides fast estimation of molecular dimer interaction energies, building upon previous CE models to address their limitations.

Background

Quantitative analysis of intermolecular interactions is essential for understanding molecular crystal packing, polymorphism, mechanical properties, and crystal growth. Traditional quantum mechanical calculations require three separate SCF calculations (dimer and two monomers), making them computationally expensive for routine analysis. The CE-1p model addresses this by avoiding the dimer SCF calculation while maintaining accuracy comparable to high-level methods.

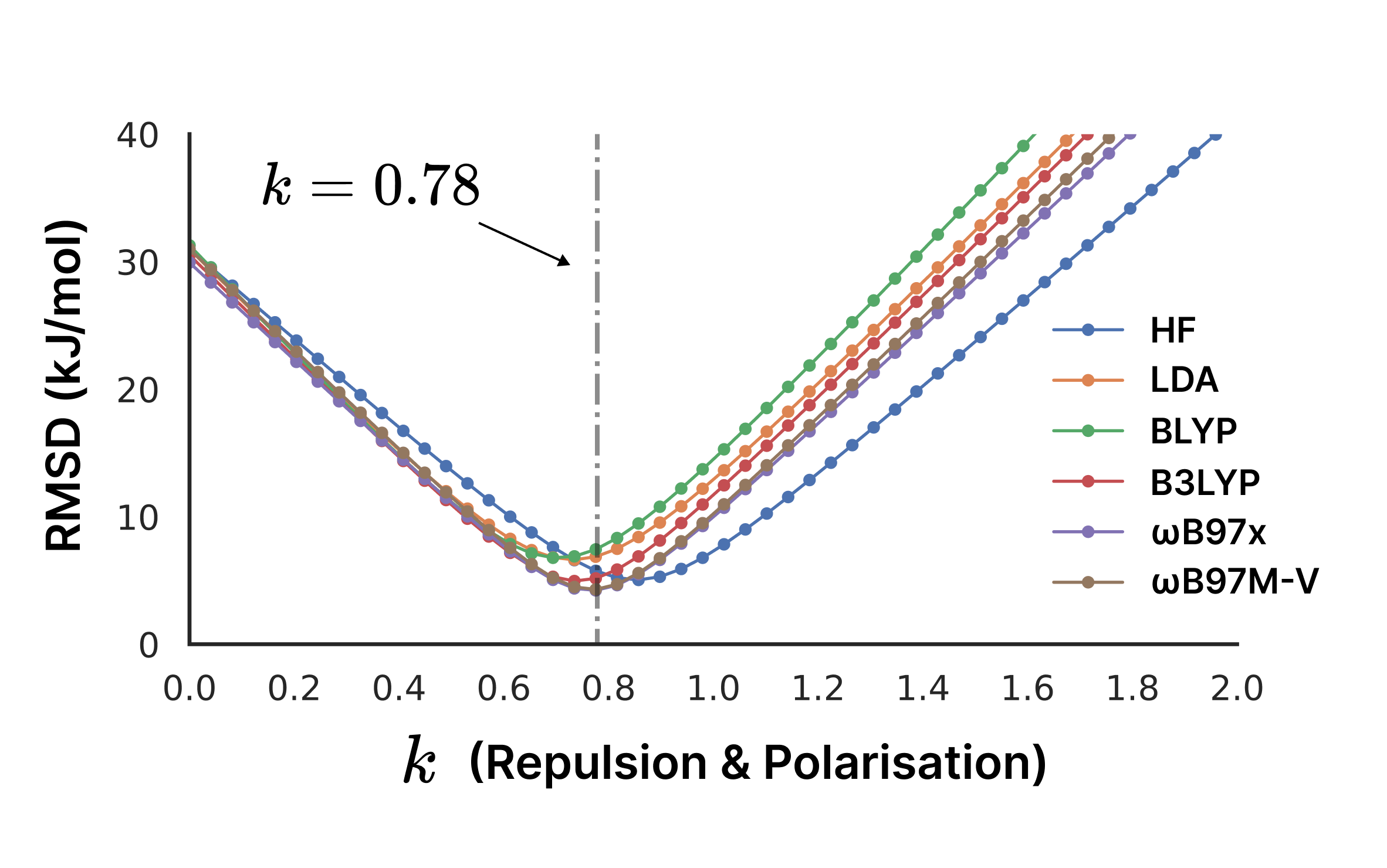
The previous CrystalExplorer models (CE-HF and CE-B3LYP) demonstrated the value of this approach but suffered from several limitations: restricted elemental coverage, global dispersion parameters that didn't depend on molecular environment, free atomic polarizabilities rather than molecular values, and multiple fitted parameters that reduced transferability. The CE-1p model addresses these issues through three key improvements. First, by supporting Effective Core Potentials (ECPs) and the def2-SVP basis set, it handles elements from hydrogen to radon, enabling application to organometallic compounds and heavy element systems. Second, it replaces the empirical D2 dispersion correction with the theoretically-motivated eXchange-hole Dipole Model (XDM), providing molecule-specific dispersion coefficients, proper treatment of anisotropic polarizabilities, and higher-order dispersion terms (C₆, C₈, C₁₀). Most importantly, CE-1p uses a single scaling factor (k = 0.78) applied to both repulsion and polarization terms, dramatically improving transferability across different wavefunction sources.

Energy Model and Implementation

The total interaction energy is calculated as a sum of physically-motivated components:

$E_\text{tot} = E_\text{coul} + k_\text{rep} E_\text{rep} + E_\text{exch} + k_\text{pol} E_\text{pol} + E_\text{disp}$

Where $E_\text{coul}$ represents Coulombic (electrostatic) interactions, $E_\text{rep}$ is repulsion from orbital orthogonalization, $E_\text{exch}$ accounts for exchange interactions, $E_\text{pol}$ is the polarization energy, and $E_\text{disp}$ captures dispersion interactions via XDM. The CE-1p model uses a single empirical parameter $k = 0.78$ that scales both the repulsion and polarization terms ($k_\text{rep} = k_\text{pol} = 0.78$), fitted to reproduce ωB97M-V/def2-QZVP interaction energies over 1157 intermolecular interactions from 147 crystal structures.

To understand the computational implementation, here are the matrix operations for each energy term:

1. Coulomb Energy ($E_\text{coul}$)

The Coulomb energy includes electron-electron, electron-nuclear, and nuclear-nuclear interactions:

$E_\text{coul} = E_{ee} + E_{en} + E_{nn} + E_{ecp}$

Where for the interaction between molecules A and B:

• Nuclear-nuclear repulsion: $E_{nn} = \sum_{i \in A} \sum_{j \in B} \frac{Z_i Z_j}{|R_i - R_j|}$
• Electron-nuclear attraction: $E_{en} = -2 \text{Tr}(D_{AB}^n V_{AB}) - (E_A^{en} + E_B^{en})$
• Electron-electron repulsion: $E_{ee} = \text{Tr}(D_{AB}^n J_{AB}) - (E_A^{ee} + E_B^{ee})$
• ECP contribution (if present): $E_{ecp} = 2 \text{Tr}(D_{AB}^n V_{ecp,AB}) - (E_A^{ecp} + E_B^{ecp})$

Here $D_{AB}^n$ is the density matrix of the non-orthogonalized dimer, $V_{AB}$ is the nuclear attraction matrix, and $J_{AB}$ is the Coulomb matrix.

2. Exchange Energy ($E_\text{exch}$)

The exchange energy arises from the antisymmetrization requirement:

$E_\text{exch} = -\text{Tr}(D_{AB}^n K_{AB}) + E_A^{exch} + E_B^{exch}$

Where $K_{AB}$ is the exchange matrix computed from the merged but non-orthogonalized molecular orbitals.

3. Repulsion Energy ($E_\text{rep}$)

The repulsion term accounts for the energy change upon orthogonalization:

$E_\text{rep} = E_{AB}^o - E_{AB}^n$

Where:

• $E_{AB}^o = \text{Tr}(D_{AB}^o H_{AB}) + \text{Tr}(D_{AB}^o J_{AB}^o) - \text{Tr}(D_{AB}^o K_{AB}^o)$
• $E_{AB}^n = \text{Tr}(D_{AB}^n H_{AB}) + \text{Tr}(D_{AB}^n J_{AB}^n) - \text{Tr}(D_{AB}^n K_{AB}^n)$

The orthogonalization is performed using symmetric Löwdin orthogonalization:

$C_{AB}^o = S_{AB}^{-1/2} C_{AB}^n$

Where $S_{AB}$ is the overlap matrix of the combined basis.

4. Polarization Energy ($E_\text{pol}$)

The polarization energy uses the electric field at atomic positions:

$E_\text{pol} = -\frac{1}{2} \sum_{i \in A} \alpha_i |\vec{F}_i^B|^2 - \frac{1}{2} \sum_{j \in B} \alpha_j |\vec{F}_j^A|^2$

Where:

• $\vec{F}_i^B$ is the electric field at atom $i$ due to molecule B
• $\alpha_i$ is the polarizability of atom $i$ (from XDM or empirical values)

The electric field has nuclear and electronic contributions:

$\vec{F}_i = \vec{F}_i^{nuc} + \vec{F}_i^{elec}$

With:

• Nuclear: $\vec{F}_i^{nuc} = \sum_{j} Z_j \frac{\vec{r}_{ij}}{|\vec{r}_{ij}|^3}$
• Electronic: $\vec{F}_i^{elec} = -2 \sum_{\mu\nu} D_{\mu\nu} \langle \phi_\mu | \frac{\vec{r}}{|\vec{r}|^3} | \phi_\nu \rangle$

5. Dispersion Energy ($E_\text{disp}$)

Using the XDM model, the dispersion energy is:

$E_\text{disp} = -\sum_{i \in A} \sum_{j \in B} \left(\frac{C_{6,ij}}{R_{ij}^6 + R_{vdW,ij}^6} + \frac{C_{8,ij}}{R_{ij}^8 + R_{vdW,ij}^8} + \frac{C_{10,ij}}{R_{ij}^{10} + R_{vdW,ij}^{10}}\right)$

Where:

• $C_{n,ij}$ are dispersion coefficients computed from atomic polarizabilities and multipole moments
• $R_{vdW,ij} = a_1 R_{crit,ij} + a_2$ with $a_1 = 0.65$ and $a_2 = 1.70$ Å
• $R_{crit,ij}$ is determined from the dispersion coefficients

The dispersion coefficients are calculated using:

$C_{6,ij} = \frac{2}{3} \frac{\alpha_i \alpha_j}{\alpha_i/N_i^{eff} + \alpha_j/N_j^{eff}}$

And higher-order terms from the multipole moments computed via XDM.

Putting it all together

The CE-1p calculation proceeds through five steps: (1) compute wavefunctions for isolated molecules A and B, (2) merge wavefunctions to create combined basis $\{A \cup B\}$ without SCF, (3) apply Löwdin symmetric orthogonalization to merged MOs, (4) compute all energy terms, and (5) apply the single parameter k = 0.78 to repulsion and polarization. The key efficiency comes from avoiding the dimer SCF calculation - while traditional methods require 3 SCF calculations (A, B, and AB), CE-1p only needs 2 SCF calculations (A and B) plus fast matrix operations. For a typical organic dimer, this translates to a ~12x speedup (from ~60 seconds to ~5 seconds).

def ce1p_energy(mol_A, mol_B, k=0.78):
    # 1. Compute monomer wavefunctions
    wfn_A = compute_wavefunction(mol_A)  # SCF for A
    wfn_B = compute_wavefunction(mol_B)  # SCF for B
    
    # 2. Merge wavefunctions (no SCF!)
    wfn_AB_n = merge_wavefunctions(wfn_A, wfn_B)
    
    # 3. Orthogonalize
    S_AB = compute_overlap(wfn_AB_n.basis)
    wfn_AB_o = orthogonalize(wfn_AB_n, S_AB)
    
    # 4. Compute energy components
    E_coul = compute_coulomb(wfn_AB_n, wfn_A, wfn_B)
    E_exch = compute_exchange(wfn_AB_n, wfn_A, wfn_B)
    E_rep = compute_repulsion(wfn_AB_o, wfn_AB_n)
    E_pol = compute_polarization(wfn_A, wfn_B)
    E_disp = compute_xdm_dispersion(wfn_A, wfn_B)
    
    # 5. Apply scaling
    E_total = E_coul + E_exch + k*E_rep + k*E_pol + E_disp
    
    return E_total

Fitting procedure

The single parameter k = 0.78 was determined through extensive fitting against a carefully curated training set of 1157 molecular/ion pairs from 147 crystal structures, including organic, inorganic, and organometallic systems with elements up to bromine, plus iodine and xenon. Reference energies were computed at the ωB97M-V/def2-QZVP level, with systems showing significant charge transfer excluded. The remarkable finding is that the optimal k value shows minimal variation across different wavefunction sources (HF, LDA, BLYP, B3LYP, ωB97X, ωB97M-V), demonstrating excellent transferability.

Performance and Validation

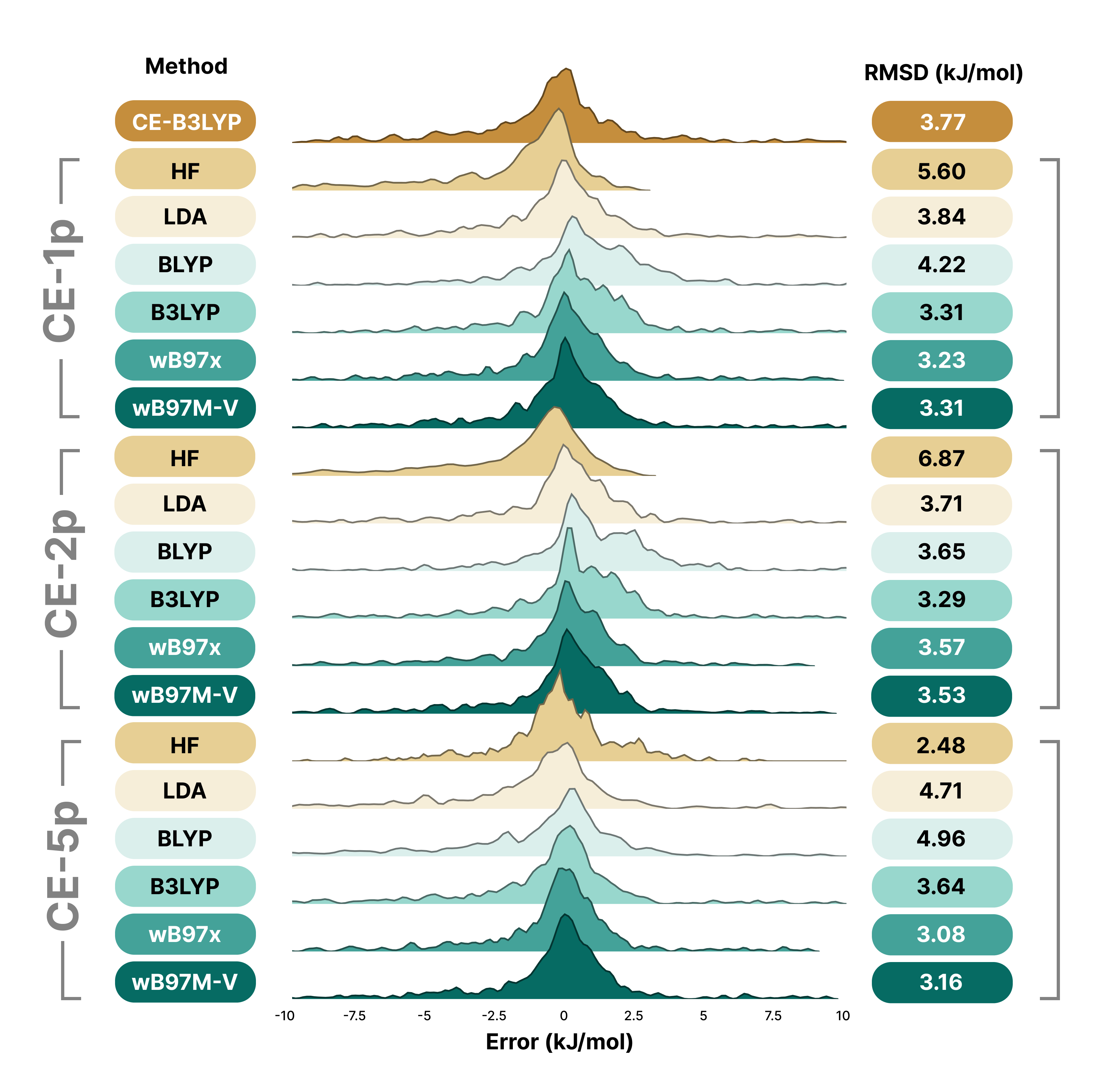
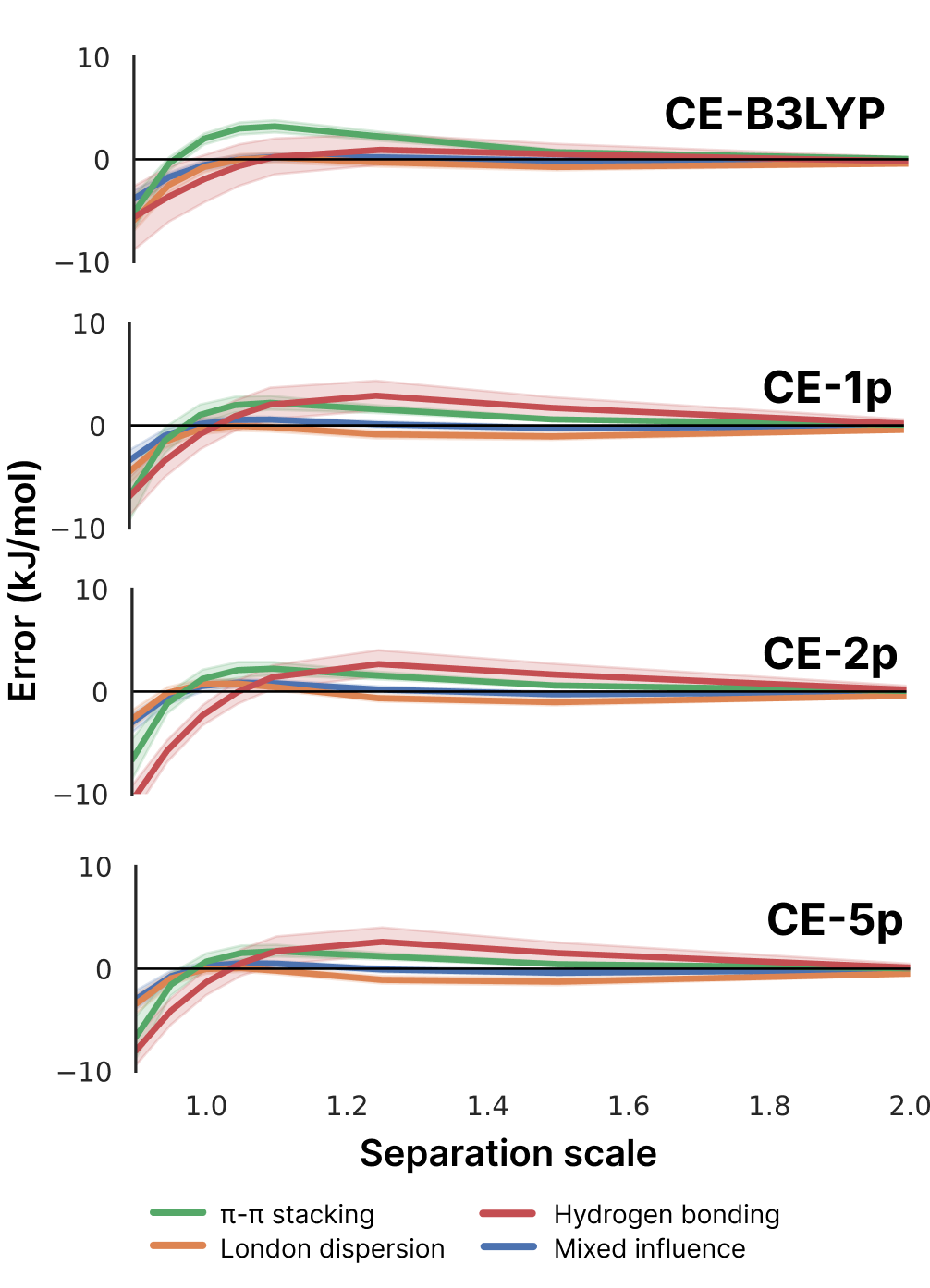
The CE-1p model demonstrates excellent performance across diverse benchmark sets. For the S66x8 benchmark of organic intermolecular interactions, CE-1p achieves RMSDs of 3.2-3.3 kJ/mol and MADs around 2.0-2.1 kJ/mol across different wavefunction sources (B3LYP, ωB97X, ωB97M-V), outperforming the previous CE-B3LYP model (RMSD 3.8, MAD 2.4 kJ/mol). For X23 molecular crystal lattice energies, CE-1p with B3LYP achieves near state-of-the-art accuracy with an MAD of 3.6 kJ/mol, significantly better than the previous CE-B3LYP (7.3 kJ/mol). The model has been validated with various wavefunction sources using the def2-SVP basis set, with B3LYP, ωB97X, and ωB97M-V performing best overall.

The paper also evaluated models with 2 parameters (CE-2p) and 5 parameters (CE-5p), finding that additional parameters provided minimal improvement while reducing transferability:

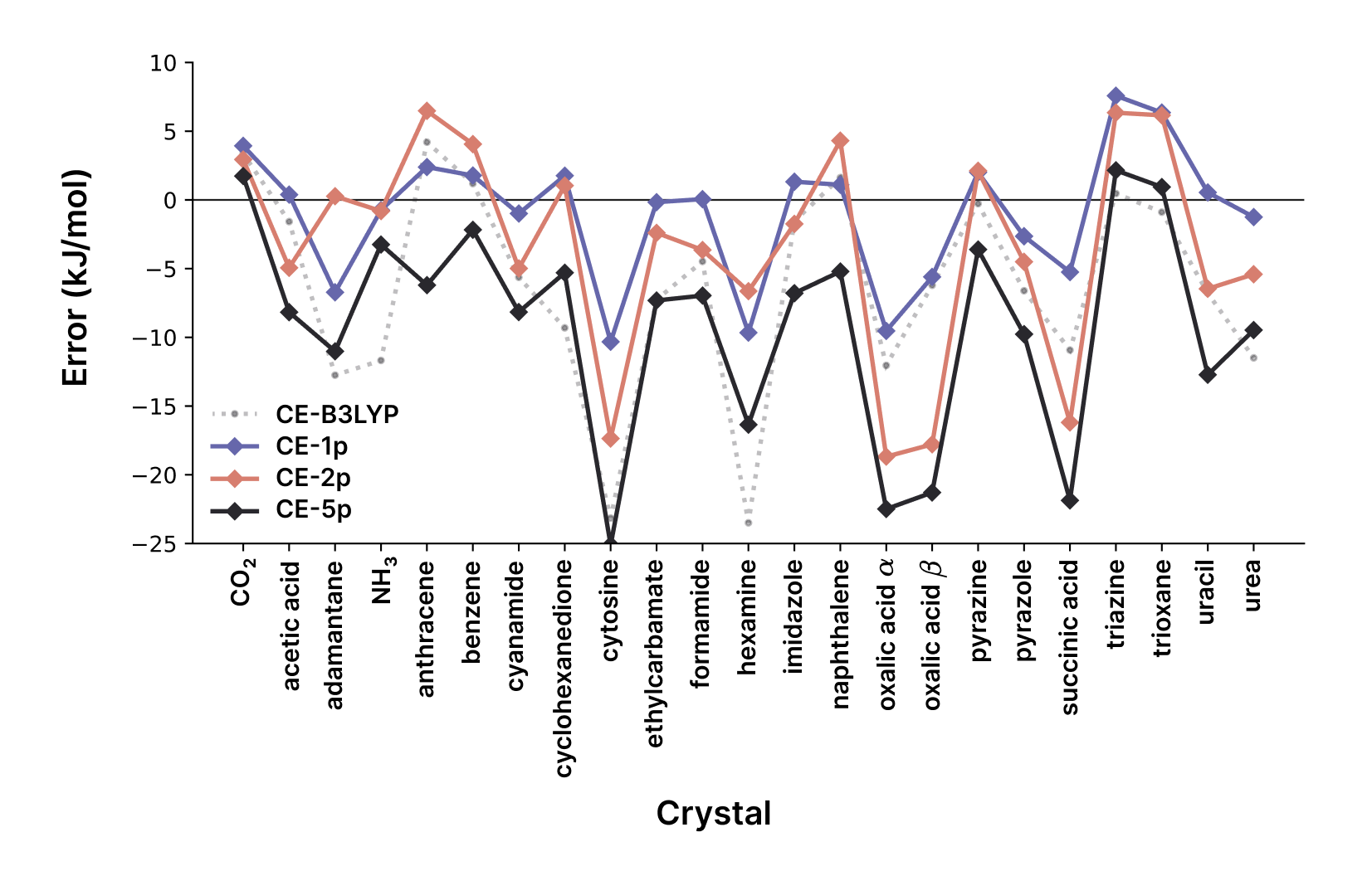
The CE-1p model is implemented in occ (open-source quantum chemistry code, GitHub) and CrystalExplorer for visualization and analysis of molecular crystals, with Python bindings available for integration with computational workflows.

Cohesive energies of molecular crystals

Lattice energies are calculated by summing pairwise interactions over the crystal using the direct summation approach:

$E^A_\text{latt} = \frac{1}{2} \sum_{|\mathbf{r}^{AB}| < r_\text{max}} E^{A B}$

Where $E^A_\text{latt}$ is the lattice energy for symmetry unique molecule $A$, $E^{AB}$ is the pairwise interaction energy between molecules $A$ and $B$, with the factor of $\frac{1}{2}$ correcting for double counting. The CE-1p model shows remarkable accuracy despite the simplicity of this approach.

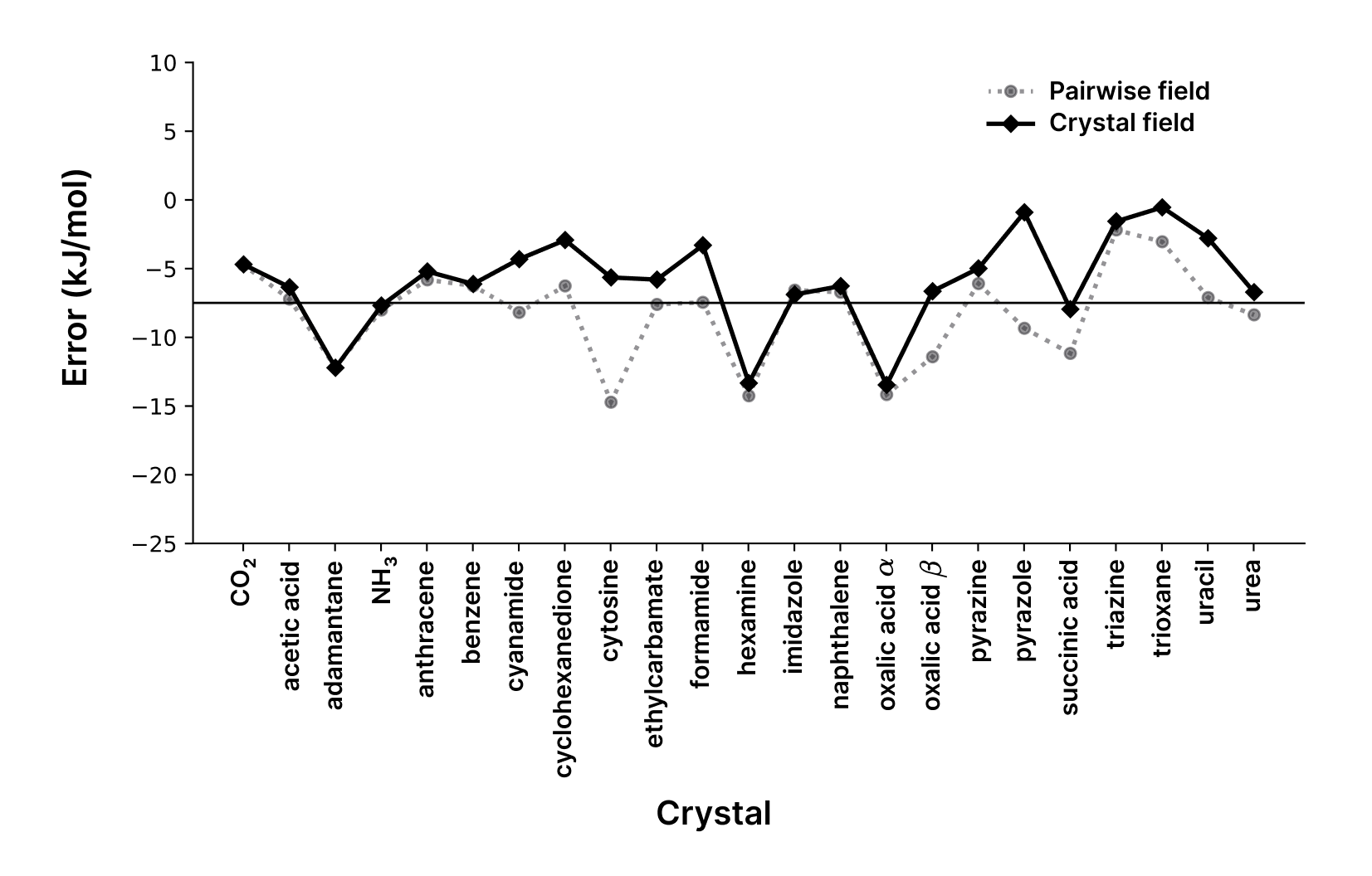
A key consideration for crystal calculations is the treatment of polarization. The standard pairwise approach can overestimate polarization, particularly for highly polar crystals. The model can optionally use crystal field polarization: $E_\text{pol}^i = -\frac{1}{2} \alpha_i | \vec{F}_i |^2$, where $\vec{F}_i$ is the total electric field from all neighbors. This correction is particularly important for systems like cytosine, where it significantly improves agreement with experimental sublimation enthalpies.

The S66x8 benchmark includes interactions at multiple separations (0.9 to 2.0 times equilibrium distance), providing insight into model behavior. The CE-1p model maintains consistent accuracy across all separations, with slight overbinding at compressed geometries. This is particularly relevant for high-pressure crystallography studies, crystal structure prediction where trial structures may have non-optimal contacts, and mechanical property calculations requiring accurate repulsive walls.

The implementation now supports direct rotation of wavefunctions in pure spherical harmonic basis sets, enabling compatibility with programs like ORCA that exclusively use these basis conventions.

Summary

The CE-1p model achieves its design goals of accuracy, efficiency, and transferability:

• Single parameter: k = 0.78 works across all tested wavefunction sources and diverse chemical systems
• Accuracy: RMSD of 3.3 kJ/mol for S66x8, MAD of 3.6 kJ/mol for X23 lattice energies
• Speed: Much faster than conventional calculations (no dimer SCF), computationally efficient
• Coverage: Applicable to elements H-Rn
• Interpretability: Meaningful energy decomposition provides physical insight

While the model has some limitations (less accurate at very short intermolecular distances, assumes minimal charge transfer between molecules, treats polarization in pairwise approximation, and requires pre-calculated monomer wavefunctions), its advantages make it an excellent choice for routine crystal structure analysis and molecular interaction studies.