1. Intermolecular Interactions: From Theory to Practice

Much of chemistry and materials science involves condensed matter, that is to intermolecular interactions (or perhaps more accurately non-bonded interactions). Understanding these interactions is therefore fundamental to many applications of computational chemistry. Since theoretical and computational chemistry is generally focused on getting the best answer in a tractable amount of computer time, it's essential to know which kinds of interactions are important for which systems, and cheap and dirty can we be in their approximation when explaining or predicting some observable phenomenon.

Gibbs Free Energy vs. Enthalpy

To cut a very long story short, we can start with the Gibbs free energy to determine whether molecular association is spontaneous under given conditions ($T$, $P$). Recall that the Gibbs free energy combines energetic and entropic contributions:

$\Delta G = \Delta H - T \Delta S$

Or more explicitly:

$\Delta G_{\text{dimer}} = \Delta H_{\text{dimer}} - T\Delta S_{\text{dimer}}$

In practice, we're often primarily concerned with predicting the enthalpy contribution because:

1. Entropy is quite often similar across related systems - For comparing similar binding modes, $\Delta S$ varies less than $\Delta H$ (and $\Delta S$ can be much harder to model...)
2. Low temperatures reduce entropic contributions - At cryogenic crystal structure conditions, $T\Delta S$ becomes small
3. Enthalpy dominates strong interactions - For hydrogen bonds and ionic interactions, $|\Delta H| >> |T\Delta S|$
4. Computational efficiency - Energy calculations on a static system directly yield energies related to enthalpy (at least much of the energy)

Hess's law: Enthalpy is path-independent

For a given molecular dimer or pair for example, this means that regardless of how they came to be in a given configuration we can calculate the enthalpy as:

$\Delta H_{\text{binding}} = H_{\text{dimer}} - H_{\text{monomer A}} - H_{\text{monomer B}}$

This can be done via electronic structure calculations, molecular mechanics force fields, tight-binding, machine learned potentials or really any method that computes the total energy for a given system:

$\Delta E_{\text{binding}} = E_{AB} - E_A - E_B$

This binding energy is not the whole picture, there are other enthalpy contributions:

$\Delta H = \Delta E + \Delta(PV) + \Delta E_{\text{ZPE}} + \Delta E_{\text{thermal}}$

For condensed phases and moderate temperatures:

• $\Delta(PV) \approx 0$ (negligible volume change)
• $\Delta E_{\text{thermal}} \approx 0$ (a common assumption)

Therefore:

$\Delta H \approx \Delta E + \Delta E_{\text{ZPE}}$

And often the zero-point energy correction is also small, giving:

$\Delta H \approx \Delta E$

This is why computational chemists often report energy calculations as approximations to enthalpies, but keep this in mind when considering systems you're working with...

(Some of) the Physics of Intermolecular Forces

Different types of interactions arise from different quantum mechanical phenomena, and most of them are approximated in molecular mechanics and force fields via analysis of the long-range or asymptotic behaviour.

Consider whether the approximations are sensible

Even in the text below I'll talk about where some effects are or are not important, but you should always consider whether that is correct and why approximations might be sensible (or not) for a given system. Nothing beats understanding the fundamental physics (QM) or actual experiments.

1. Electrostatic (Coulomb) Interactions

Coulomb interaction between partial charges

The classical electrostatic energy between charges $q_i$ and $q_j$ separated by distance $r_{ij}$:

$E_\text{elec} = \sum_{i<j} \frac{q_i q_j}{r_{ij}}$

That is if we just work in atomic units so we can do away with the constant factor of $\frac{1}{4\pi\epsilon_0}$

This is fundamentally important for condensed matter, as it's the longest-range interaction (i.e. slowest to decay to 0), decaying as $1/r$.

If we instead had a multipole series:

$E_{\text{elec}} = E_{\text{charge-charge}} + E_{\text{charge-dipole}} + E_{\text{dipole-dipole}} + ...$

This stems from the Taylor expansion of the Coulomb interaction. Most force-fields don't even bother considering dipoles, but few if any include terms beyond quadrupoles.

These point charges can be placed wherever you see fit, though the mathematics for e.g. forces becomes much simpler if they are at atomic sites i.e. partial charges. Indeed we can approximate e.g. atomic dipoles, quadrupoles etc. through partial charges around the atoms (in the limit, we have a full electron density distribution).

2. Exchange-Repulsion (Pauli Exclusion)

Pauli repulsion prevents orbital overlap

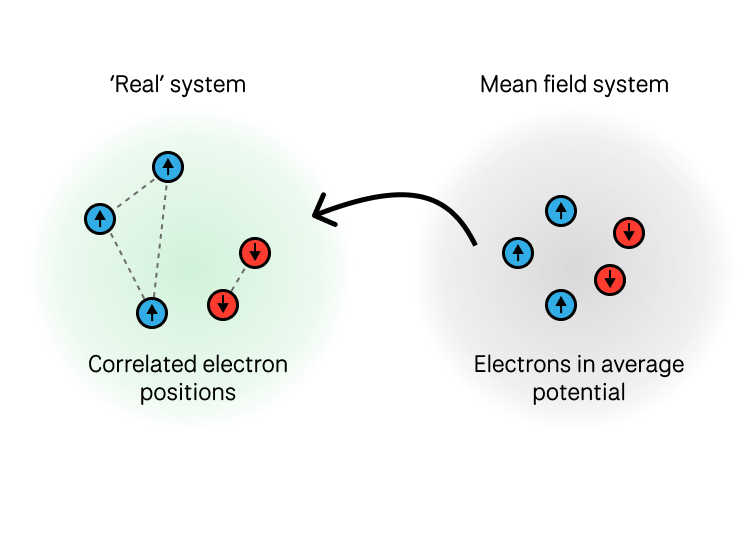
When electron clouds overlap, the Pauli exclusion principle requires antisymmetrization of the wavefunction, leading to repulsion:

$E_{\text{exch}} \propto \text{exp}(-\alpha r)$

This short-range repulsion prevents molecular interpenetration. This is the source of the $\text{exp}(-\alpha r)$ term in Buckingham potentials and many others. The Lennard Jones potential is effectively approximating this as $1/r^{12}$

3. Polarization (Induction)

Electric field inducing molecular polarization

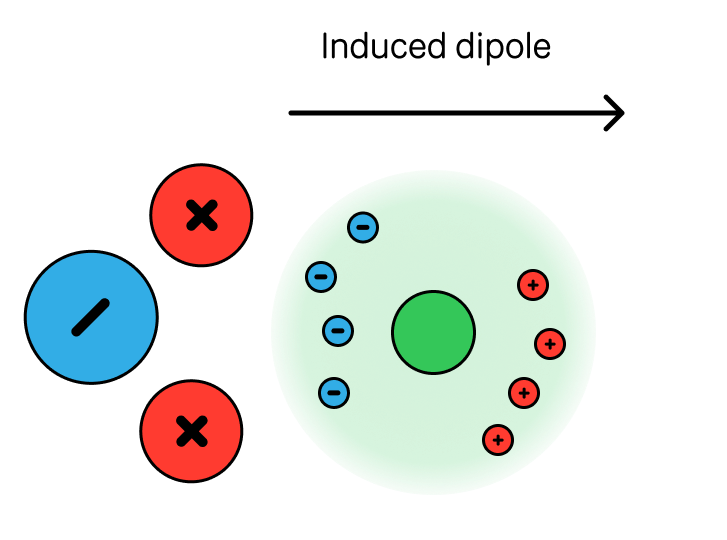
The electric field of molecule A induces a dipole in molecule B:

$E_{\text{ind}} = -\frac{1}{2}\alpha_B |E_A|^2$

where $\alpha_B$ is the polarizability of molecule B. This scales as $r^{-4}$ for charge-induced dipole interactions. While this formula provides a useful approximation, it's important to remember that polarizability is effectively a volume term, and this approach assumes the polarizable volume of a site is spherical/isotropic.

4. Dispersion (London Forces, van der Waals)

London dispersion from correlated electron fluctuations

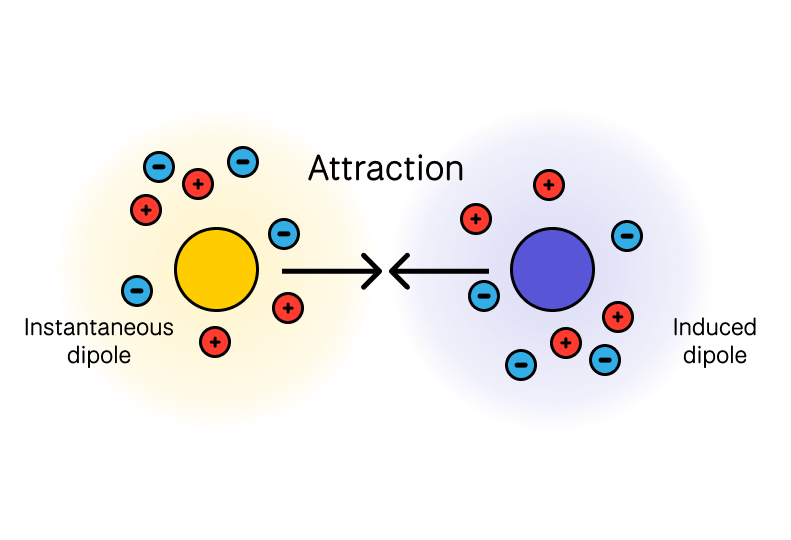
Perhaps the most important kind of intermolecular interaction to consider due to its pervasiveness is London Dispersion!

All molecules interact via quantum mechanical fluctuations in electron density:

$E_{\text{disp}} = -\frac{3}{2}\frac{I_A I_B}{I_A + I_B}\frac{\alpha_A \alpha_B}{r^6}$

where $I$ represents ionization potentials. This $r^{-6}$ attraction is universal.

People frequently refer to this as a weak interaction, but its ubiquity means that for many molecular crystals for example it's the most important energetic term...

A classical example: the argon dimer

The Lennard-Jones potential showing repulsive and attractive regions

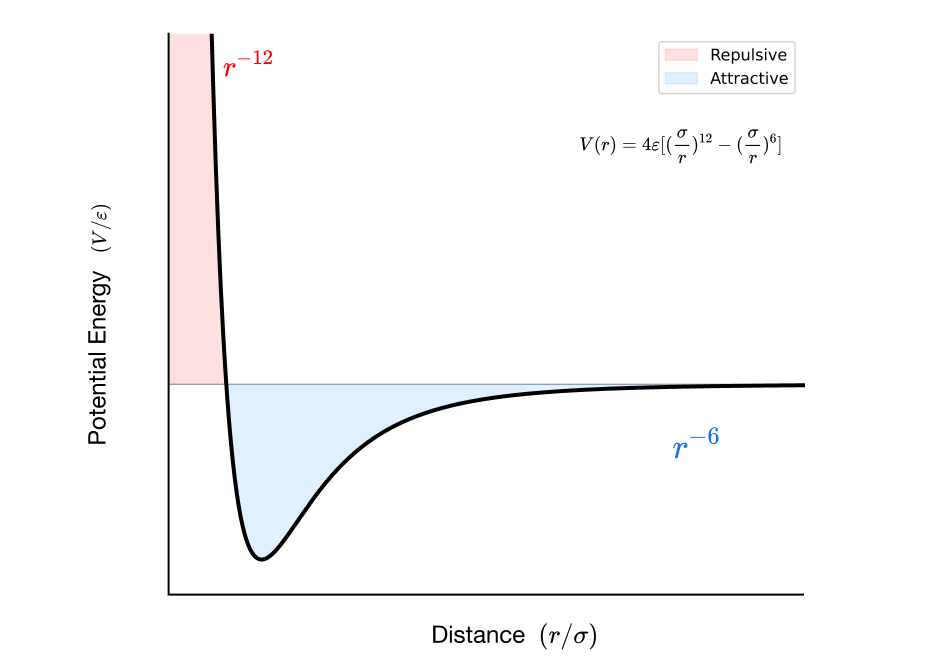
For noble gases like argon, only dispersion and exchange-repulsion really matter. The Lennard-Jones potential captures this physics:

$V_{LJ}(r) = 4\epsilon\left[\left(\frac{\sigma}{r}\right)^{12} - \left(\frac{\sigma}{r}\right)^6\right]$

Where:

• $\epsilon$ = well depth (attraction strength)
• $\sigma$ = distance where $V_{LJ} = 0$
• $r^{-12}$ term models exchange-repulsion
• $r^{-6}$ term models dispersion

For Ar-Ar:

• $\epsilon = 0.996$ kJ/mol
• $\sigma = 3.401$ Å
• $r_{\text{min}} = 3.816$ Å

The $r^{-12}$ repulsion is empirical; more accurate potentials use exponential forms.

This works well for a number of reasons, but it's also quick to calculate! Don't need to take a square root when computing distances, $r^{12} = (r^6)^2$ etc.

Combining Rules for Mixed Interactions

These parameters and their physical interpretation also lead to so-called combining rules. When atoms of different types interact, combining rules can be used determine their interaction parameters - this makes fitting a force field require less parameters, be less likely to overfit and much else.

Lorentz-Berthelot rules (most common):

• $\sigma_{ij} = \frac{\sigma_{ii} + \sigma_{jj}}{2}$ (arithmetic mean of sizes)
• $\epsilon_{ij} = \sqrt{\epsilon_{ii} \epsilon_{jj}}$ (geometric mean of well depths)

Physical justification:

• Size parameter ($\sigma$): Contact distance is roughly additive
• Energy parameter ($\epsilon$): Well depth relates to $\sqrt{I_i I_j}$ from dispersion theory

Example for O-H interaction:

• If $\epsilon_O = 0.65$ kJ/mol and $\epsilon_H = 0.016$ kJ/mol
• Then $\epsilon_{OH} = \sqrt{0.65 \times 0.016} = 0.10$ kJ/mol
• If $\sigma_O = 3.17$ Å and $\sigma_H = 2.65$ Å
• Then $\sigma_{OH} = (3.17 + 2.65)/2 = 2.91$ Å

There are of course many other combining rules...

Hands on case study: the water dimer

With all that in mind, let's examine a water dimer. Water dimers showcase all four interaction types. The hydrogen bond involves:

1. Electrostatic attraction between O(-) and H(+)
2. Exchange-repulsion at short distances
3. Polarization as the H-bond enhances dipoles - we're going to ignore this in our force field
4. Dispersion between electron clouds

An interactive force field for the water dimer.

The interactive visualisation below demonstrates combining rules in action. You can adjust Lennard-Jones parameters and partial charges, and and see how they affect the energy of the dimer at different separations.

Use this interactive tool to consider the following questions:

1. How correlated are the parameters? I.e. if we change the charge can we adjust something else to compensate
2. Can we get the right energy at equilibrium without the right behaviour in general?
3. Is it enough to focus on a 1-dimensional slice of the potential energy surface for a water dimer if we were to use this force field for e.g. liquid water?

Interactive Water Dimer Energy Calculator

Parameters

Charges

q(H): 0.417 e

q(O) = -0.834 e

O-O Parameters

ε: 0.636 kJ/mol

σ: 3.151 Å

H-H Parameters

ε: 0.0157 kJ/mol

σ: 2.649 Å

Energy Components (@1.00)

Loading...

All values in kJ/mol

Computational Exercises

At it's core, the most simple way to compute a pair energy is via the previously mentioned energy difference:

$E_\text{interaction} = E_\text{AB} - E_\text{A} - E_\text{B}$

i.e. we'd need 3 calculations, one for each monomer and one for the pair!

However, in the case of isolated molecules we also need to relax (geometry optimise) each component individually in order to have a fair comparison and an accurate interaction energy.

About geometry optimisation

Throughout these exercises we're going to ignore the relaxation aspect of interactions. It is important, but it makes the calculations take longer and it's just more things to worry about for now. So just pretend it's all there, but keep in mind for the future especially for flexible molecules this can be a major component of the energy.

Exercise 1: Basic Interaction Energy Calculation

Understanding how molecules interact is fundamental to computational chemistry. We'll calculate the interaction energy between two water molecules using the supermolecular approach: $\Delta E = E_\text{AB} - E_\text{A} - E_\text{B}$.

Basic Water Dimer Interaction Energy▼

Calculate the interaction energy between two water molecules using HF/3-21G to understand hydrogen bonding.

0/4 completed

Step 1: Navigate to the basic directory

Instructions

Navigate to the directory containing the water molecule geometries and set up for the calculation.

Commands

cd awscc_workshop_2025/01_pair_energies/basic/
ls -la *.xyz

Expected Output

A.xyz  B.xyz  AB.xyz

Notes

A.xyz and B.xyz contain individual water molecules, AB.xyz contains the dimer.

Exercise 2: Basis Set Superposition Error (BSSE) Correction

When calculating interaction energies, basis set superposition error (BSSE) can lead to overestimation of binding. The Boys-Bernardi counterpoise correction addresses this by using ghost atoms to ensure consistent basis sets.

The source of this error is basically that the electrons have more degrees of freedom to relax when the basis set size increases, so if we have a complete basis set for each monomer then there should ideally be no BSSE!.

BSSE Correction with Counterpoise Method▼

Calculate BSSE-corrected interaction energy for water dimer using the Boys-Bernardi counterpoise procedure with ORCA.

0/5 completed

Step 1: Navigate to the BSSE directory

Instructions

Navigate to the BSSE directory and examine the multi-job input file that performs all necessary calculations.

Commands

cd ../BSSE/
ls -la
head -20 bsse.inp

Expected Output

# Calculations for Boys-Bernardi CP correction
#

# --------------------------------------------
# First the monomer. In principle, you only need
# to run it once, but we keep it for clarity.
# --------------------------------------------
! hf 3-21g VeryTightSCF PModel
%id "monomer"
* xyz 0 1
O   -0.702196054  -0.056060256   0.009942262
H   -1.022193224   0.846775782  -0.011488714
H    0.257521062   0.042121496   0.005218999
*

Notes

The file contains 5 calculations: 2 monomers, 1 dimer, and 2 ghost calculations. If we adjust that to a larger basis set we should see smaller BSSE!

Exercise 3: CE-1P Pairwise Interaction Model

The CE-1P (CrystalExplorer - 1 parameter) model provides physically motivated construction of of interaction energies into electrostatic, exchange, repulsion, polarisation, and dispersion components, useful for understanding the nature of intermolecular interactions.

CE-1P Interaction Energy Decomposition▼

Calculate and decompose water dimer interaction energy using the CE-1P model in OCC to understand the physical components of hydrogen bonding.

0/5 completed

Step 1: Navigate to the CE1P directory

Instructions

Navigate to the CE1P directory and examine the structure. CE-1P requires wavefunction files from SCF calculations.

Commands

cd ../CE1P/
ls -la
cat README.md | head -10

Expected Output

A.xyz  B.xyz  AB.xyz  A.owf.json  run_ce1p.sh  translate.toml  README.md

This folder contains an example of the CE1P pairwise model interaction energy decomposition.

The script will:
1. Run SCF calculations on monomers A and B
2. Generate wavefunction files (.owf.json)
3. Run CE-1P decomposition

Notes

The .owf.json files store wavefunctions needed for the CE-1P analysis.

Method Comparison Summary

Method	Binding Energy (kJ/mol)	Time	Key Advantage
HF/3-21G	-43.64	~0.5 sec	Very fast, but poor accuracy
HF/3-21G (BSSE-corr)	-25.64	~7 s	Systematic improvability, well benchmarked
CE-1P (ωB97X/def2-SVP)	-24.69	<0.5 sec	Cheap, accurate, physical insight

Why do the methods give different binding energies?

• HF/3-21G the direct supermolecule method overestimates binding due to small basis set (BSSE)
• HF/3-21G w/BSSE provides good balance, but can be very expensive for larger dimers
• CE-1P includes all physical components explicitly, giving more accurate results

Key physical insights for water dimer:

1. Coulomb dominates (117% of binding) - quantum penetration effects
2. Dispersion is modest (9%) but probably essential for accurate binding

Key Takeaways

✓ Thermodynamic foundations: Binding energy connects to thermodynamics through Hess's law

✓ Four(ish) fundamental interactions to consider: Electrostatic, exchange-repulsion, polarization, and dispersion govern intermolecular interactions

✓ Distance dependence: Each force has distinct distance dependence and physical origin

✓ Complex interplay: Real molecules exhibit complex interplay of all forces

✓ Computational methods: Must account for dispersion, things like BSSE

✓ Method choice matters: Speed vs. accuracy trade-offs for different applications. Error cancellation means a 'better' method isn't always better.

Suggested Extension: Advanced Energy Decomposition with LED

Advanced Energy Decomposition with LED

For those interested in a more sophisticated energy decomposition analysis, Local Energy Decomposition (LED) provides detailed insights into intermolecular interactions at the coupled cluster level.

Local Energy Decomposition (LED) Analysis

LED decomposes DLPNO-CCSD(T) energies into physically meaningful components. This method is available in ORCA and provides highly accurate interaction energies with detailed breakdowns.

You can check this out in the LED directory, or looking at the ORCA documentation